Model merging and task arithmetic have emerged as promising scalable approaches to merge multiple single-task checkpoints to one multi-task model, but their applicability is reduced by significant performance loss. Previous works have linked these drops to interference in the weight space and erasure of important task-specific features. Instead, in this work we show that the information required to solve each task is still preserved after merging as different tasks mostly use non-overlapping sets of weights. We propose TALL-masks, a method to identify these task supports given a collection of task vectors and show that one can retrieve >99% of the single task accuracy by applying our masks to the multi-task vector, effectively compressing the individual checkpoints. We study the statistics of intersections among constructed masks and reveal the existence of selfish and catastrophic weights, i.e., parameters that are important exclusively to one task and irrelevant to all tasks but detrimental to multi-task fusion. For this reason, we propose Consensus Merging, an algorithm that eliminates such weights and improves the general performance of existing model merging approaches. Our experiments in vision and NLP benchmarks with up to 20 tasks, show that Consensus Merging consistently improves existing approaches. Furthermore, our proposed compression scheme reduces storage from 57Gb to 8.2Gb while retaining 99.7% of original performance.
A paradigm shift has occured in the last few years with the development of foundation models and the release of fine-tuned checkpoints stemming from them. From the seed of one pre-trained model, e.g. CLIP, multiple checkpoints are available online for many different tasks. In multi-task model merging or task arithmetic, the goal is to merge these single-task checkpoints into one multi-task model. However, the performance of the merged model is often significantly lower compared to the single-task models.
The main takeaways of the paper are:
Setup: Assume a pretrained model \(f(\boldsymbol{x}; \boldsymbol{\theta}_0)\) where \(\boldsymbol{x}\) is the input and \(\boldsymbol{\theta}_0\) are the pre-trained weights. We fine-tune the model on \(T\) tasks, obtaining the fine-tuned weights \(\boldsymbol{\theta}_t=\boldsymbol{\theta}_0 +\boldsymbol{\tau}_t, \forall t\in[T]\), where \(\boldsymbol{\tau}_t\) are the task-vectors. Given these task vectors, the goal is to merge them into one multi-task vector \(\boldsymbol{\tau}_{\text{MTL}}\) and this can be done with various methods, such as task arithmetic (TA) or TIES. The final model with parameters \(\boldsymbol{\theta}=\boldsymbol{\theta}_0 + \boldsymbol{\tau}_{\text{MTL}}\) is then a multi-task model.
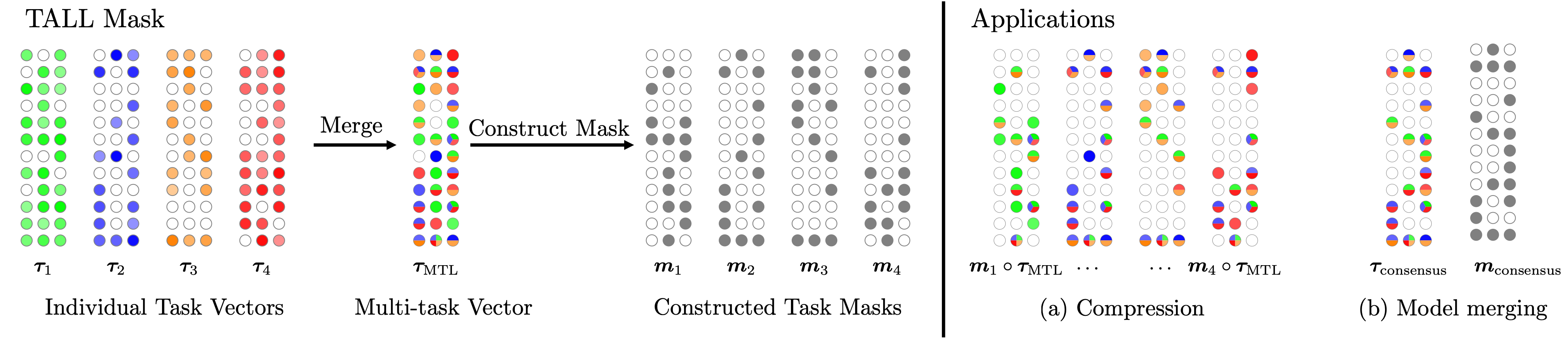
Localizing task-specific information. We aim to find the weights in the multi-task vector \(\boldsymbol{\tau}_{\text{MTL}}\) that are important for each task. We do this by developping a sparse binary mask \(\boldsymbol{m}_t\) for each task \(t\) that approximates functionally the original task vector \(\boldsymbol{\tau}_t\). The mask is defined as: \begin{align} \boldsymbol{m}_t = \unicode{x1D7D9} \left\{|\boldsymbol{\tau}_t| \geq |\boldsymbol{\tau}_{\text{MTL}} - \boldsymbol{\tau}_t| * \lambda_t \right\} \end{align} where \(\lambda_t\) is a threshold parameter that controls the sparsity of the mask and is set via a held-out validation set.
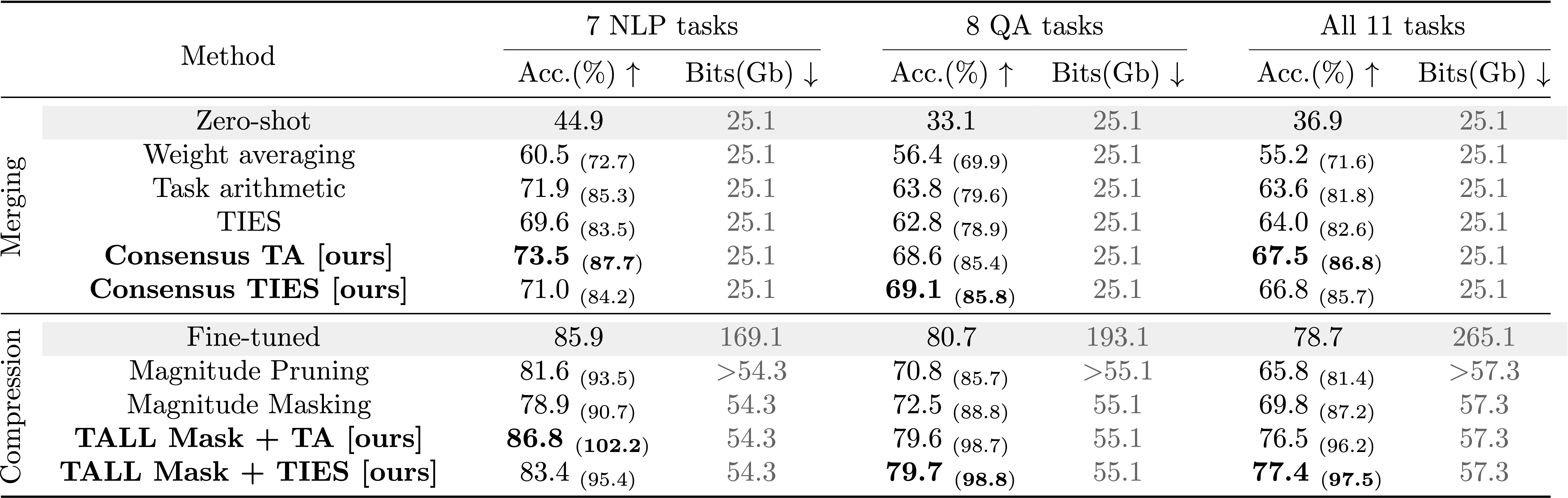
Application 1: Compression. Surprisingly, using the model with parameters \(\boldsymbol{\theta}_0 + \boldsymbol{m}_t \circ \boldsymbol{\tau}_{\text{MTL}}\) we can retrieve >99% of the original performance compared to the original model with parameters \(\boldsymbol{\theta}_t= \boldsymbol{\theta}_0 + \boldsymbol{\tau}_t\). This has immediate implications for compression as we only need to store \(\boldsymbol{\tau}_{\text{MTL}}\), \(\boldsymbol{m}_t, \forall t \in [T]\) and the zeroshot model \(\boldsymbol{\theta}_0\) instead of all the fine-tuned checkpoints \(\boldsymbol{\theta}_t, \forall t\in[T]\).
Application 2: Improving model merging. Given the task-specific binary masks, it is interesting to study the intersection of the masks among tasks. Do tasks use many of the same parameters? Are there weights deemed important only by one task? Or none? Turns out that this is the case and we observe the existence of selfish and catastrophic weights, i.e., parameters that are important exclusively to one task and irrelevant to all tasks. We propose the Consensus Merging algorithm that eliminates these weights and improves the performance for multi-task model merging:
\begin{align} \boldsymbol{m}_\textrm{consensus} = {\LARGE \unicode{x1D7D9}} \left\{ \sum_{t\in[T]} \boldsymbol{m}_t \geq k\right\} \end{align} and the final multi-task vector is obtained by element-wise multiplication of the consensus mask with the underlying merged vector: \begin{align} \boldsymbol{\tau}_\textrm{consensus} = \boldsymbol{m}_\textrm{consensus} \circ \boldsymbol{\tau}_{\text{MTL}} \end{align}Natural Language Processing: Eliminating the catastrophic and selfish weights leads to significant gains in performance for all three cases. For example, augmenting TIES with our proposed method in the case of 8 Q&A tasks leads to 6.9% absolute performance improvement.
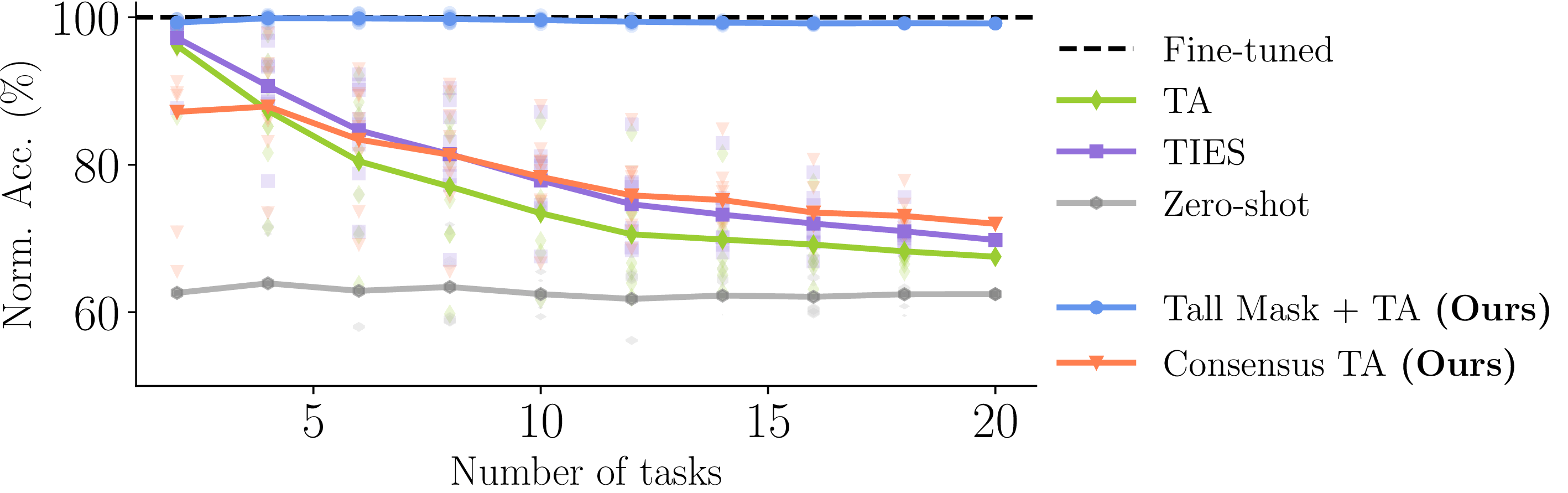
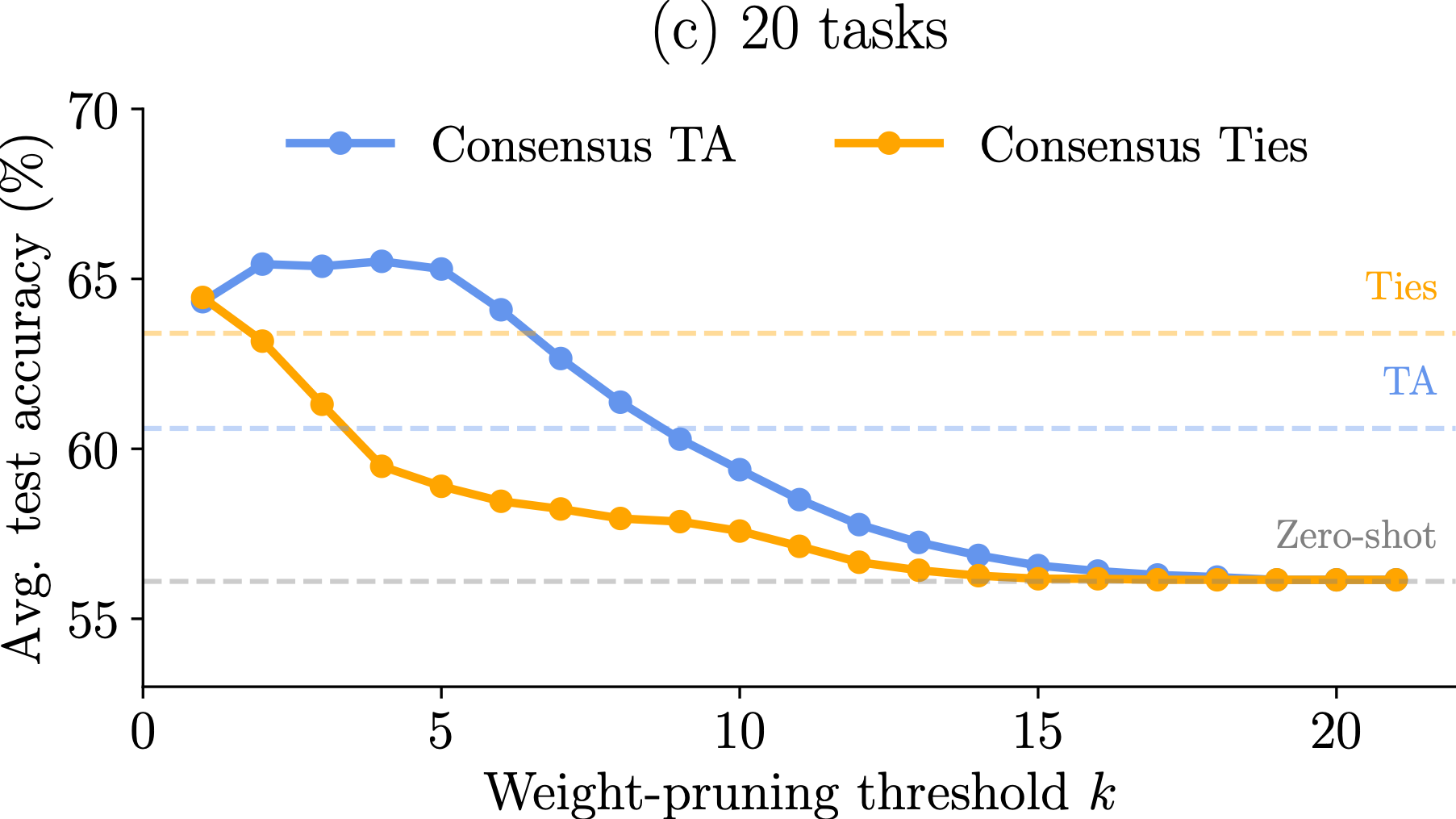
Computer Vision: Our compression scheme is robust to the increase in the number of tasks; even for 20 tasks all model sizes achieve 99% performance retention. Also, our model merging method outperforms the baselines, especially as the number of tasks and the model size increase.
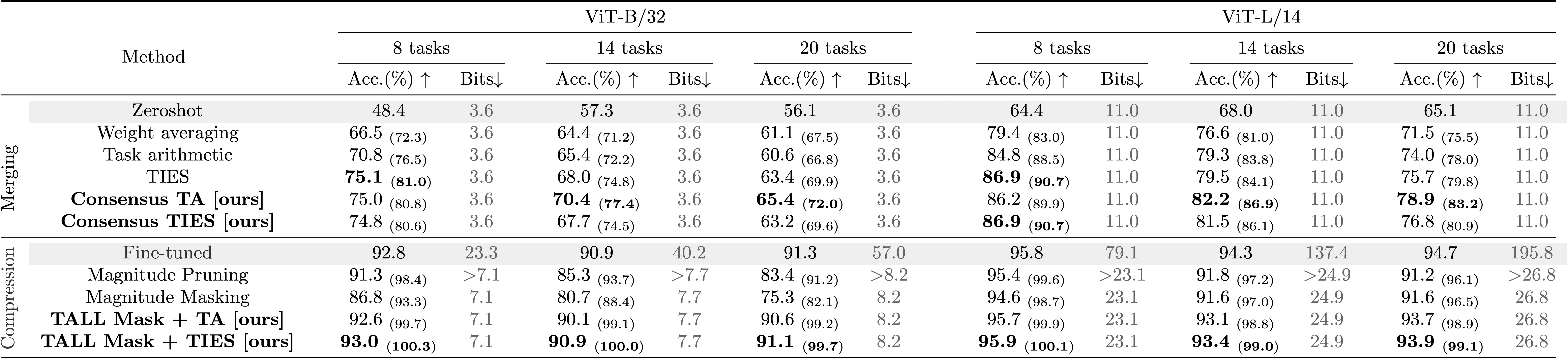
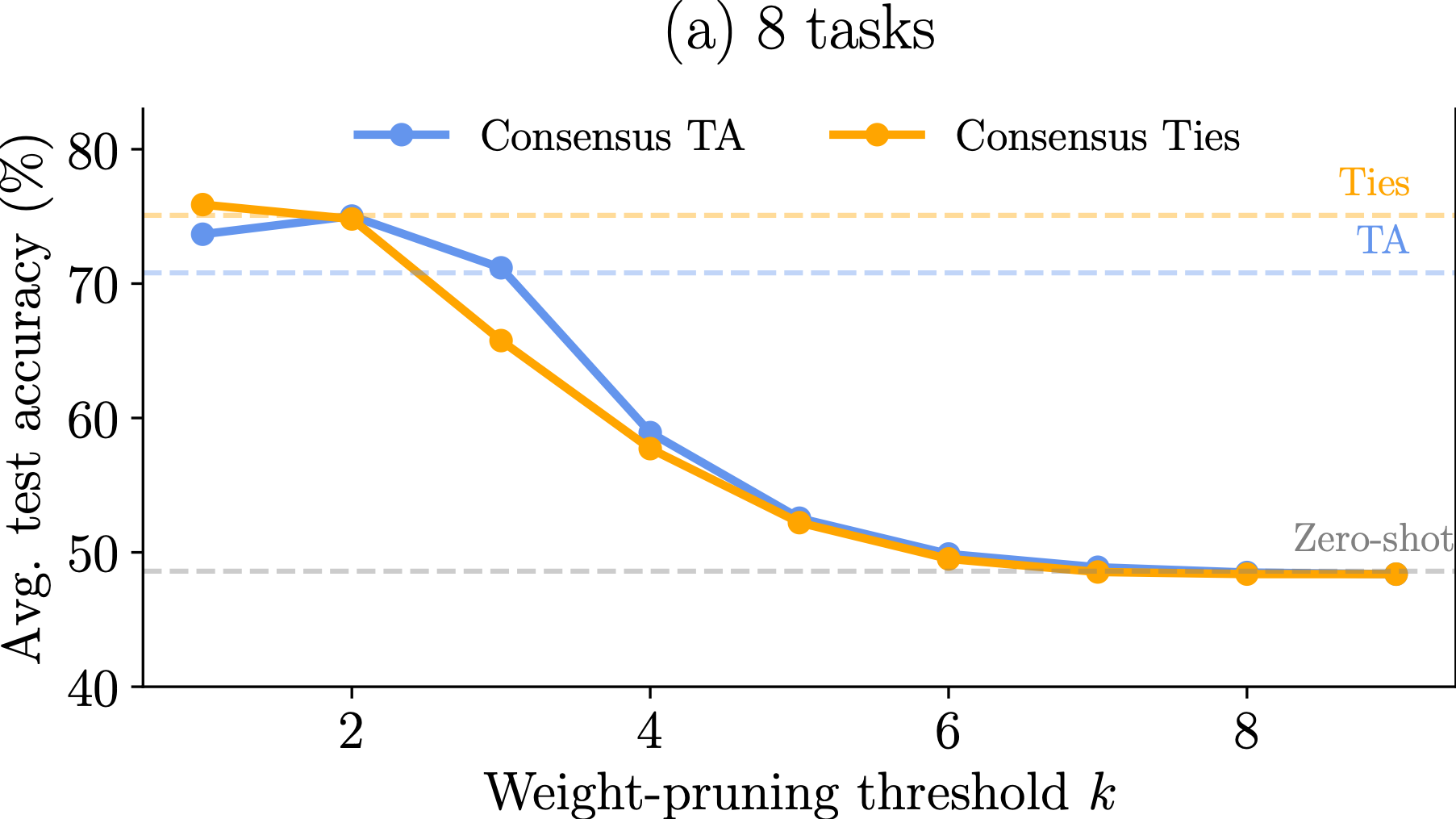
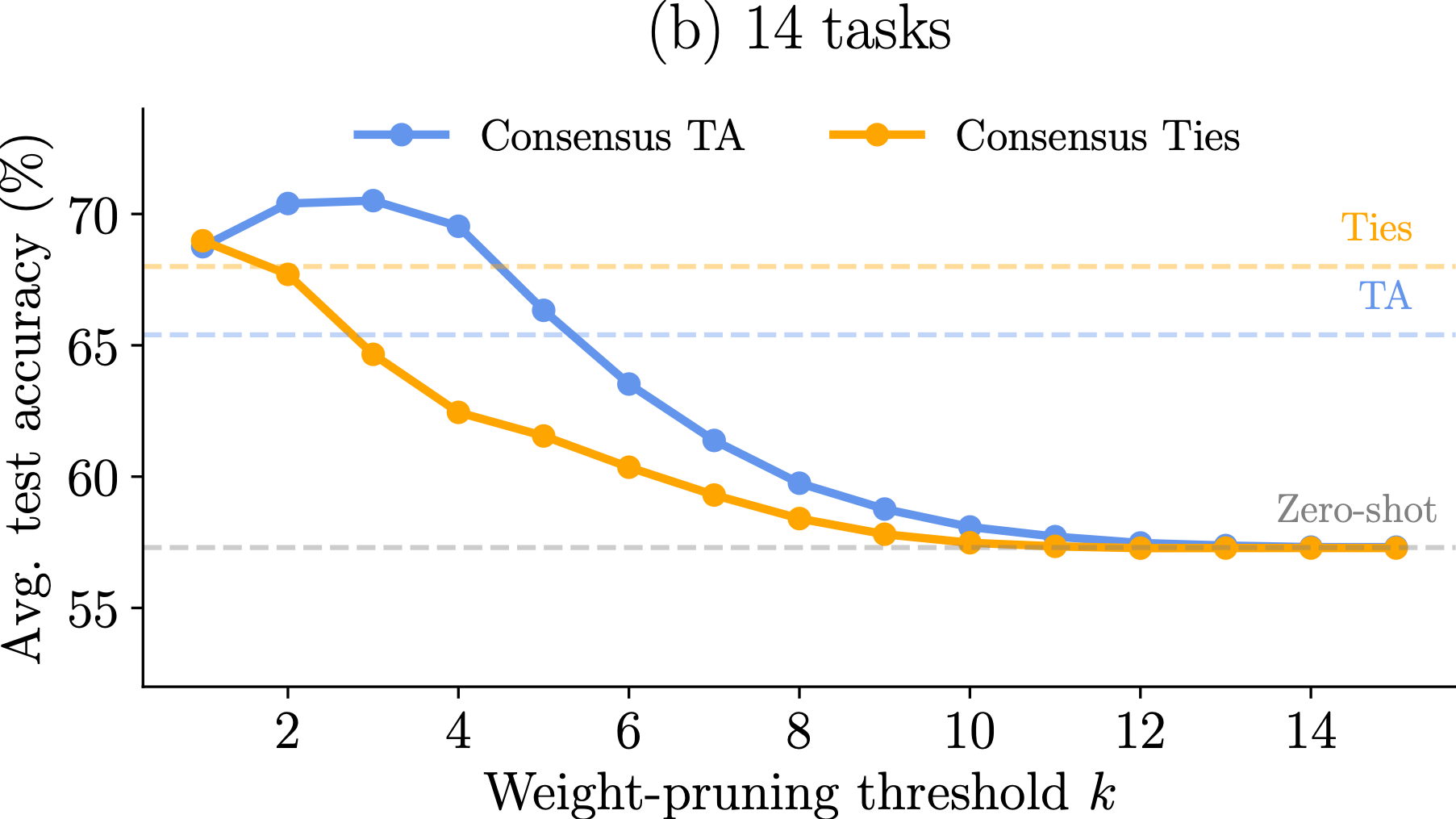
Observation 1: For all three computer vision benchmarks (8, 14 and 20 tasks), TALL-masks is able to retrieve almost the full performance of the single-task models, while eliminating catastrophic and selfish weights improves the performance of the merged model compared to baselines for all tasks.
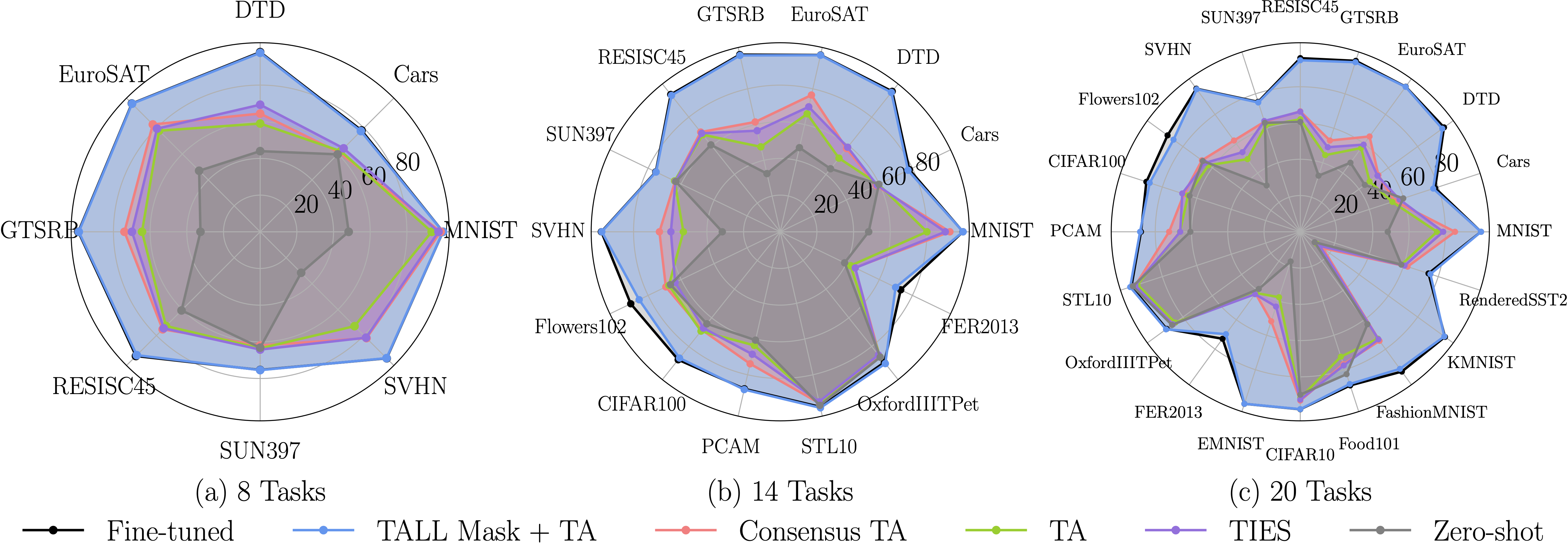
Observation 2: Different model merging methods result in different allocation of important parameters across tasks. For instance, TIES aligns a significant portion of the paramaters so that they are deemed imporant by all tasks. The mask agreement profile varies as the number of tasks increases.
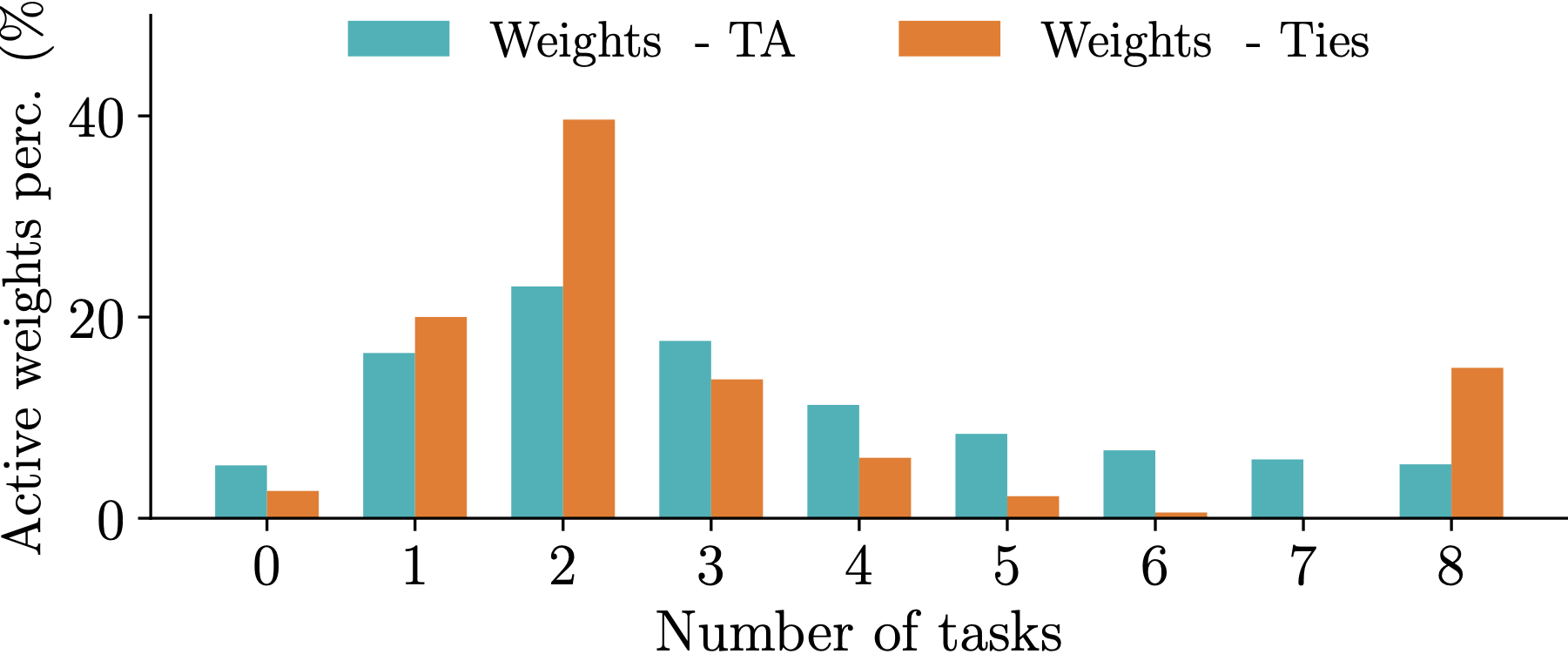
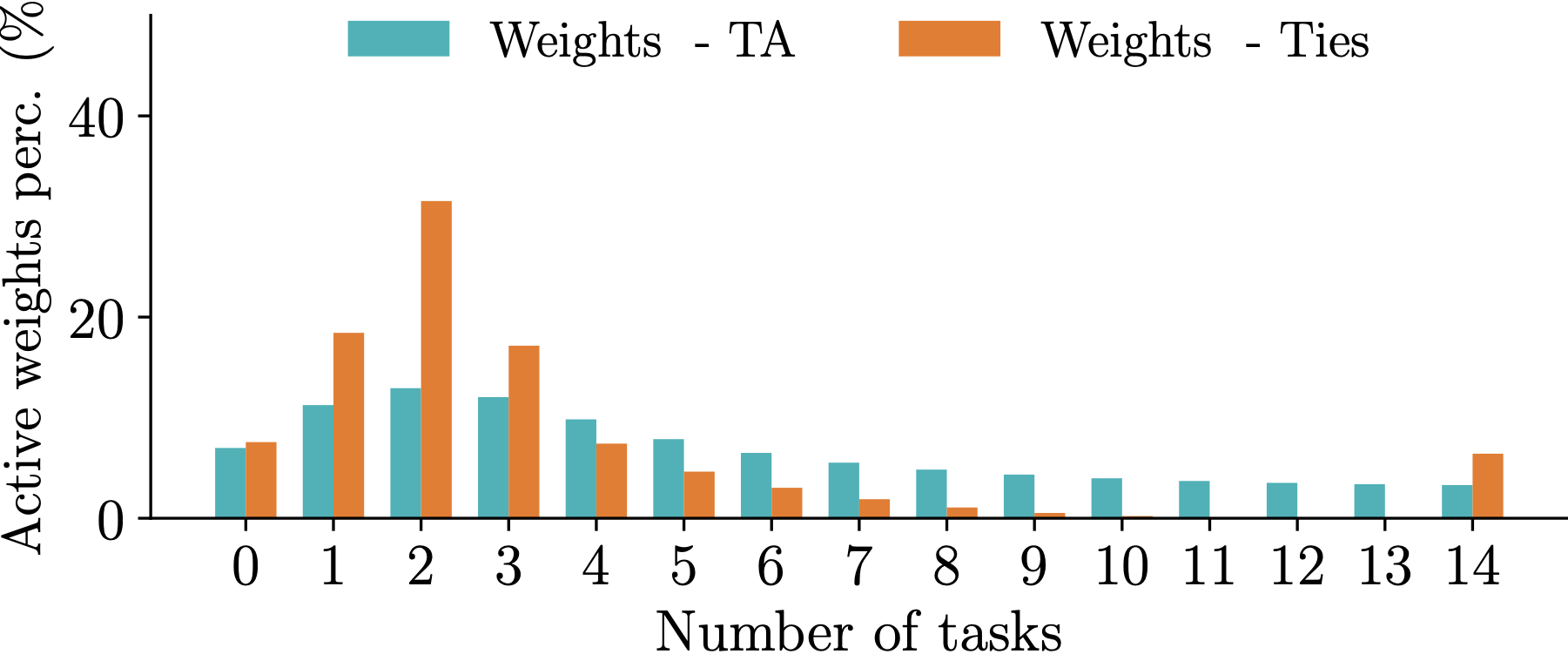
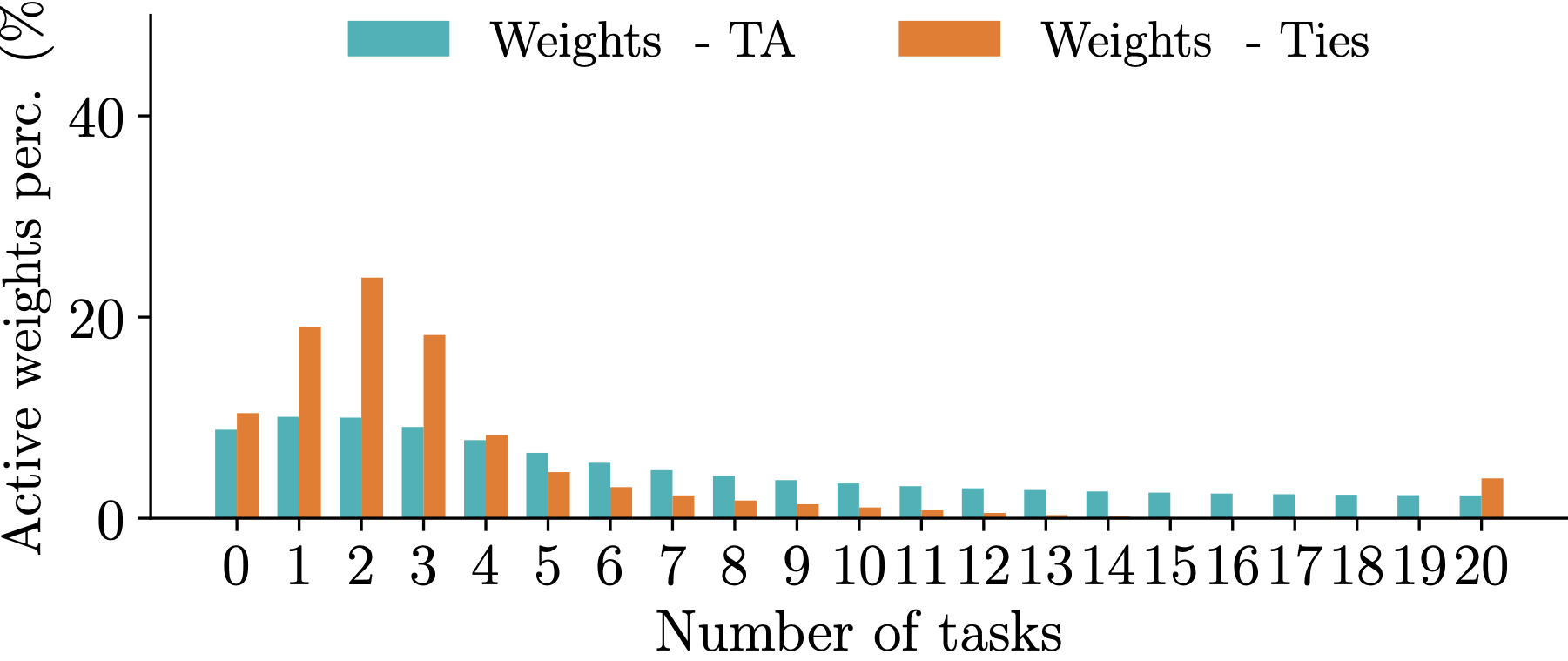
Observation 3: The difference in mask agreement profiles leads to different performance of merged models as more and more parameters are discarded. The behavior depends on the number of tasks but TIES is more sensitive thatn Task Arithmetic (TA).
@inproceedings{wang2024localizing,
title={Localizing Task Information for Improved Model Merging and Compression},
author={Wang, Ke and
Dimitriadis, Nikolaos and
Ortiz{-}Jim{\'{e}}nez, Guillermo and
Fleuret, Fran\c{c}ois and
Frossard, Pascal},
booktitle={International Conference on Machine Learning},
year={2024}
}